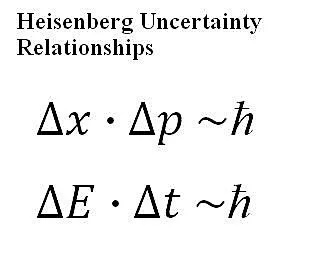home | what's new | other sites | contact | about

  

 

Word Gems 

exploring self-realization, sacred personhood, and full humanity

 

Quantum Mechanics

What is Heisenberg's Uncertainty Principle?

 

 

return to "Quantum Mechanics" main-page

 

 

from https://www.thoughtco.com/the-heisenberg-uncertainty-principle-2699357

 

Heisenberg's uncertainty principle is one of the cornerstones of quantum physics, but it is often not deeply understood by those who have not carefully studied it. While it does, as the name suggests, define a certain level of uncertainty at the most fundamental levels of nature itself, that uncertainty manifests in a very constrained way, so it doesn't affect us in our daily lives. Only carefully constructed experiments can reveal this principle at work.

In 1927, the German physicist Werner Heisenberg put forth what has become known as the Heisenberg uncertainty principle (or just uncertainty principle or, sometimes, Heisenberg principle). While attempting to build an intuitive model of quantum physics, Heisenberg had uncovered that there were certain fundamental relationships which put limitations on how well we could know certain quantities. Specifically, in the most straightforward application of the principle:

The more precisely you know the position of a particle, the less precisely you can simultaneously know the momentum of that same particle.

Heisenberg Uncertainty Relationships

Heisenberg's uncertainty principle is a very precise mathematical statement about the nature of a quantum system. In physical and mathematical terms, it constrains the degree of precision we can ever talk about having about a system. The following two equations (also shown, in prettier form, in the graphic at the top of this article), called the Heisenberg uncertainty relationships, are the most common equations related to the uncertainty principle:

    Equation 1: delta- x * delta- p is proportional to h-bar
    Equation 2: delta- E * delta- t is proportional to h-bar

The symbols in the above equations have the following meaning:

h-bar: Called the "reduced Planck constant," this has the value of the Planck's constant divided by 2*pi.

delta-x: This is the uncertainty in position of an object (say of a given particle).

delta-p: This is the uncertainty in momentum of an object.

delta-E: This is the uncertainty in energy of an object.

delta-t: This is the uncertainty in time measurement of an object.

From these equations, we can tell some physical properties of the system's measurement uncertainty based upon our corresponding level of precision with our measurement. If the uncertainty in any of these measurements gets very small, which corresponds to having an extremely precise measurement, then these relationships tell us that the corresponding uncertainty would have to increase, to maintain the proportionality.

In other words, we cannot simultaneously measure both properties within each equation to an unlimited level of precision. The more precisely we measure position, the less precisely we are able to simultaneously measure momentum (and vice versa). The more precisely we measure time, the less precisely we are able to simultaneously measure energy (and vice versa).

A Common-Sense Example

Though the above may seem very strange, there's actually a decent correspondence to the way we can function in the real (that is, classical) world. Let's say that we were watching a race car on a track and we were supposed to record when it crossed a finish line. We are supposed to measure not only the time that it crosses the finish line but also the exact speed at which it does so. We measure the speed by pushing a button on a stopwatch at the moment we see it cross the finish line and we measure the speed by looking at a digital read-out (which is not in line with watching the car, so you have to turn your head once it crosses the finish line). In this classical case, there is clearly some degree of uncertainty about this, because these actions take some physical time. We'll see the car touch the finish line, push the stopwatch button, and look at the digital display. The physical nature of the system imposes a definite limit upon how precise this can all be. If you're focusing on trying to watch the speed, then you may be off a bit when measuring the exact time across the finish line, and vice versa.

As with most attempts to use classical examples to demonstrate quantum physical behavior, there are flaws with this analogy, but it's somewhat related to the physical reality at work in the quantum realm. The uncertainty relationships come out of the wave-like behavior of objects at the quantum scale, and the fact that it's very difficult to precisely measure the physical position of a wave, even in classical cases.

Confusion about the Uncertainty Principle

It's very common for the uncertainty principle to get confused with the phenomenon of the observer effect in quantum physics, such as that which manifests during the Schrodinger's cat thought experiment. These are actually two completely different issues within quantum physics, though both tax our classical thinking. The uncertainty principle is actually a fundamental constraint on the ability make precise statements about the behavior of a quantum system, regardless of our actual act of making the observation or not. The observer effect, on the other hand, implies that if we make a certain type of observation, the system itself will behave differently than it would without that observation in place.

 

Werner Heisenberg:

“[In most science experiments] we have to do with things and facts, with phenomena that are just as real as any phenomena in daily life. But the atoms or the elementary particles themselves are not as real; they form a world of potentialities or possibilities rather than one of [hard-edged] things or facts.”

“If one wants to give an accurate description of the elementary particle. . .the only thing which can be written down as description is a probability function. But then one sees that not even the quality of being … belongs to what is described.”

“It was about three o'clock at night when the final result of the calculation [which gave birth to quantum mechanics] lay before me ... At first I was deeply shaken ... I was so excited that I could not think of sleep. So I left the house ... and awaited the sunrise on top of a rock.”

“I think that modern physics has definitely decided in favor of Plato. In fact the smallest units of matter are not physical objects in the ordinary sense; they are forms, ideas which can be expressed unambiguously only in mathematical language.”

“The ontology of materialism rested upon the illusion that the kind of existence, the direct 'actuality' of the world around us, can be extrapolated into the atomic range. This extrapolation is impossible, however.”

“The very act of observing disturbs the system.”

“The structure underlying the phenomena is not given by material objects like the atoms of Democritus but by the form that determines the material objects. The Ideas are more fundamental than the objects.”

“Every experiment destroys some of the knowledge of the system which was obtained by previous experiments.”

“By getting to smaller and smaller units, we do not come to fundamental or indivisible units. But we do come to a point where further division has no meaning.”

“Science no longer is in the position of observer of nature, but rather recognizes itself as part of the interplay between man and nature. The scientific method ... changes and transforms its object: the procedure can no longer keep its distance from the object.”

“Only a few know, how much one must know, to know, how little one knows.”

“What we observe is not nature itself, but nature exposed to our method of questioning.”

“Not only is the Universe stranger than we think, it is stranger than we can think.”

“The reality we can put into words is never reality itself.”

Explaining his Uncertainty Principle,” he said: "Uncertainty is NOT ‘I don't know.’ It is ‘I can't know.’ ‘I am uncertain’ does not mean ‘I could be certain’."

“I believe that the existence of the classical ‘path’ can be pregnantly formulated as follows: The ‘path’ comes into existence only when we observe it.”

“Looking at something changes it.”

 “The more precise the measurement of position, the more imprecise the measurement of momentum, and vice versa.”

“...separation of the observer from the phenomenon to be observed is no longer possible.”

 

from the documentary “Atomic Physics and Reality”:

John Bell: “There is a famous sentence [from Bohr], something like, ‘Although there is no influence of one experiment on the other, there is a change in the very conditions of the possibilities of knowledge’ … a very well-turned sentence which, I believe, Bohr took a great deal of trouble in formulating and whose meaning is absolutely obscure to me. But, what I get out of Bohr’s replay, and certainly what Einstein got out of Bohr’s reply, was simply the insistence that we have no right to a picture of the atomic world.”

Editor’s note: What did Bohr mean with “there is a change in the very conditions of the possibilities of knowledge”? An altering of the “possibilities of knowledge” suggests that reality is a plastic entity, moldable, non-rigid. It seems to me that Bohr caught a glimpse of the fluidic potential of Nature itself, and man’s expansive, creative capacities to negotiate it.

 

 

 

Editor's last word:

See more discussion of Heisenberg on the "theory of everything" page