home | what's new | other sites | contact | about

Word Gems 

exploring self-realization, sacred personhood, and full humanity

Quantum Mechanics

return to "Quantum Mechanics" main-page

from the website http://www.bottomlayer.com/bottom/reality/RealityFrame1.html 

II. Computer Particles

Consider the lowly pixel. A pixel is a dot. The word comes from a loose combination of two words, picture and element. A pixel, therefore, is an element of a picture. In particular, a computer-generated picture. The basic idea has long been used in newspaper photos, and because newspaper photos are printed at a relatively low resolution, you can see the individual dots by looking closely at the photo. In a higher resolution picture (in a good magazine photo, for example), you have to look more closely, but the dots or pixels are still there. Computers similarly create images by building them up, one dot at a time.

Many pixels of different colors, distributed in different densities, make up a picture, an image. Computer monitors work on this principle. So do computer printers.

     The computer monitor is a simple example of how a computer constructs the most complex graphics (pictures) from the lowly pixel. Computer monitors are the sons and daughters of television sets. They work by sending an electron beam from the back of the picture tube, until it strikes the flat (more or less) front of the tube. The front of the picture tube is coated with a fluorescent material which glows briefly when the electron beam strikes it. By carefully focusing the electron beam, only a single, very small dot appears on the screen. This small dot is the pixel.

     The resolution of the picture at the screen -- that is, how sharp a picture will appear -- is determined primarily by how many dots make up the picture. The more dots, the sharper the picture, and you can see this by comparing a newspaper photo to a glossy magazine photo. Assuming that both pictures are in black and white, the main difference is in how many dots per inch make up the picture. To give you an idea of how many dots make up a picture, let's take a look at my home computer monitor. My monitor is set for the low end of the current standard range of resolutions, which is 640 x 480 dots. That is, whatever appears on the moniter is made up of a grid of pixels 640 dots wide and 480 dots high. That means that the total picture area of the monitor is made up of 307,200 pixels in all. Although this seems like a very large number, I can still look closely at the monitor and see all the little dots on the screen.

     In order to create color pictures, the computer (like the television set) uses the well understood fact that all humanly perceived colors are combinations of just three "primary" colors: red, blue and green.  By combining red, blue and green in various amounts, we can create any other color. For example, we create a basic yellow by mixing red and green in equal parts; purple is red and blue in equal parts; and so on. White is all three primary colors in equal parts. Black is the absence of any color.

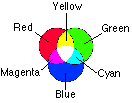
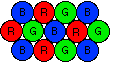
By a quirk of human visual perception, it turns out that we do not need actually to mix the colors. Instead, we can place pure red, green and blue dots so close to each other that the human eye cannot distinguish between them; the result is that the colors appear to run together, giving the impression of thousands or millions of colors, depending on how strongly we light up the red, green and blue dots. The computer screen, like the screen of a color TV, then looks like this in close up:

     The reason the computer can do this is that the human eye works on the same principle. The eye has clusters of "cones," and each cone responds to one of the three primary colors; our perception of color is determined by how many cones of each color are responding to the light. So we see that the computer is only duplicating the process of the human eye. Just as it is interesting to contemplate how the computer can create the impression of millions of colors when, in fact, it is using only millions of identical dots in only one of three colors, so it is interesting to contemplate how our own perception of continuous color turns out to be only millions of neurons, each representing only one of only three colors. The human eye, then, is "digitized" in the same way that a computer picture is digitized, and the impression of continuity is created by the fact that the level of detail in the picture is finer than the eye can distinguish.

     The pixels that make up any computer graphic can be a metaphor for the "particles" that make up the world around us. Consider these characteristics of the pixel:

·  There are just three kinds of pixels: red, green, and blue. All color graphics are only large collections of various combinations of these three types of pixel. In the same way, we say that all "things" in our world are made up of a limited number of "particles," such as electrons, protons and neutrons.

• Every red pixel is exactly like every other red pixel, and the same is true of blue and green pixels. In the same way, every electron is exactly like every other electron, and the same is true of every proton and every neutron, and every other quantum unit. (The remarkable sameness of every quantum unit has been mentioned briefly earlier in this book, and will be discussed in greater detail later.)

·  The vast and seemingly limitless variety of computer graphics -- ranging from letters of the alphabet (computer fonts) to reproductions of Michaelangelo paintings -- are created by the simple process of calculated placement of one or more of these three types of pixels. In the same way, the vast and seemingly limitless variety of materials -- ranging from earth to air to fire to water, and including solid metals (iron), liquid metals (mercury), solid liquids (glass), and human DNA, to name a randomly chosen few -- are created by the simple process of joining one or more of the basic quantum units in a variety of combinations.

Thus, for example, we think of helium as the gas we use to blow up a balloon and make it fly away; we think of plutonium as the radioactive element which powers atomic bombs. These elements appear to be completely different materials; however, the only difference between helium (He) and plutonium (Pu) is the number of protons, neutrons and electrons in each, and their arrangement in the respective atoms.

     So we see in the the computer pixel an example of how we can create a vast and limitless variety of information displays using a relatively few basic elements, changing only their arrangement. We also have an example of how discrete, individual elements can be "blurred together" by perception, even while they remain completely separate in fact. It is this perceptual blurring that creates both the variety of the display, and the impression of smooth continuity. At this level of analysis, the smoothness, the continuity, and the information content of the display itself is "illusion"; the green, red, and blue dots are "reality."

What is a pixel? By its nature, a pixel is the product of a calculation. The computer's programming instructs the hardware that, upon such-and-such conditions, it should fire its electron beam at a particular point on the monitor's screen. Where the beam hits, the fluorescent coating of the monitor screen glows, and this is perceived by the user as a dot on the screen.

     The reason the computer would do such a thing is to display information to the user who is sitting at the computer's monitor. What information? Any information the computer has in its memory. The information could be words, in which case it would use the pixels to form letters, words and sentences. The information could be pictures, in which case the pixels would form images. The information could be mathematical relationships, in which case the pixels might form wavy lines that shape up into graphs (like the sine wave graphs we have used as illustrations). Whatever information the computer has, it may use the pixels to display.

     What happens to the pixel -- or the word or the image or the graph -- when you turn off the monitor? In one sense, it ceases to exist; that is, you no longer see the pixel on the screen or anywhere else, and you will not find it no matter how hard you look. In another sense, the pixel continues to exist just as much as it ever did; that is, it still exists as a product of the programming, a potential dot on the screen which will reappear when you turn on the monitor. In this sense, the pixel is not so much a dot as it is the mathematical formula or algorithm that instructs the computer where to place dots when called upon to do so. To the computer, the important thing is the information. The pixel is only a way to display the information to the user.

     Of course, to you, the user, the information itself is quite useless without the pixel to display the information. Imagine that a brilliant computer scientist has devised a program which will answer the questions of how to produce a just and lasting peace for the world, and how to produce food, shelter and uplifting entertainment in such abundance that no person will ever lack for anything. Now imagine further that the program is run on a computer, and the computer produces the answers -- but there is no monitor to display the answer. No monitor, no sound, no printer, no ticker tape readout, no nothing -- in short, no way for the computer to display the answer to any user. To obtain such answers, we might be willing to take the computer apart diode by diode; but we would disassemble the entire computer without ever discovering the answer, because the internal state of the machinery would not reveal anything about the programming or the results of the computer's calculations, i.e., the answers. To the conventional computer, the answer has been produced and its job is done; it is up to the user to connect and turn on the monitor. To you, this state of affairs is no different from having no answer at all.

     Which is more "real" -- the formula (the programming), or the dots displayed on your monitor? Which is more useful? Which is more fundamental to the overall operation of the computer? These are meant as rhetorical questions. Plainly, if we think of the computer as a machine that processes information for the benefit of the user, then the programming and the display are equally important. We would never be able to understand how a computer works and what it does by studying only the pixels that appear on the monitor screen. Indeed, if we focused exclusively on the pixels, and thought of the pixels as the only thing that was "real," we would surely end up completely baffled by the comings and goings of these little dots. We could coin a new cliché -- instead of "She can't see the forest for the trees," we could say, "She can't see the programming for the pixels."

     Pixels -- whether displayed on a monitor or printed on paper -- are the "particles" of a computer operation. In one sense, they are and always will remain just little dots, meaningless in themselves. In another sense, they are the method by which the computer conveys its information to the user according to the agreed conventions of human perception. In a final sense, they are the products of the computer's calculations, determined by the programming, existing as "thoughts" in the computer regardless of whether they are displayed to the user.

III. Computer Properties

     We can imagine something akin to "properties" in a computer model by expanding on the display generated by pixels. Each pixel in the display can vary by (1) where it is placed, and (2) how brightly it is lit. Therefore, each pixel has a "location property" and a "brightness property." If we consider each grouping of three colored pixels (red, green, and blue) as a unit, then we can say that each such unit has a "location property," and that the overall unit has a "color property." However, the "color property" of the "pixel unit" consists fundamentally of the mixture of red, green, and blue for that unit. Each "pixel unit," therefore, can be fully described with the following set of properties:

Location property of pixel unit (x,y)

Brightness property of red pixel within pixel unit (rb)

Brightness property of green pixel within pixel unit (gb)

Brightness property of blue pixel within pixel unit (bb)

     Using these properties as our complete description of the pixel unit, we can say that the definition of a pixel unit is as follows: a "pixel unit" is a collection of three pixels located at coordinates x,y, consisting of a red pixel with brightness rb, a green pixel with brightness gb, and a blue pixel with brightness bb. This will be our formula for a pixel unit. We can now describe every one of the approximately 24.5 million pixel units on the monitor screen with just one formula, and we have used only 35 words. And we can now describe any individual pixel unit among these 24.5 million pixels using just 5 numbers: the x coordinate, the y coordinate, and the brightness of the red, green, and blue pixels (rb, gb, and bb).

     In the simple algebra of computer programming, these "properties" are the variables in the formula. Think of it as a fill-in-the-blanks exercise:

The pixel unit is located at coordinates ___, ___, consisting of a red pixel with brightness ___, a green pixel with brightness ___, and a blue pixel with brightness ___.

You fill in the blanks with any numbers you like, and you have a complete description of some pixel unit, located somewhere, with some overall color property.

     The computer can -- and usually does -- set limits on what you fill in. The most obvious limit in the above example is that you must fill in a number. That is, you may not fill in the blank with a letter, the name of your dog, a mystical runic symbol, or a Michaelangelo painting. My computer also insists that the number must be a whole number, i.e., 0, 1, 2, 3, 4, . . ., not 1.7695 or any other decimal or fraction. Also, the number must be a positive number, because the computer does not know what to make of a negative value for any of these numbers. ("Take away some red? B-but I didn't put any red there in the first place!?") Furthermore, the computer will usually define a range for the value of the variable. The graphics programs I use limit the range of red, green, and blue to whole, positive numbers between 0 and 65,535.

     As a practical matter, the x and y coordinates ordinarily will be limited by the size of the monitor and its resolution. In the example of my computer monitor, the x coordinate would have to be between 0 and 6,400 to fit on the screen, and the y coordinate between 0 and 3,840, because there are only that number of pixels across and down. However, the computer doesn't really care whether the pixel fits on the screen or not; it would be just as happy to keep track of a pixel located several feet to the right of the computer monitor. So, for example, if I entered an x coordinate with a value of 9,600, it would be located "offscreen," about five inches to the right of my monitor's screen. This is not a problem for the computer. The computer will treat such an offscreen pixel on an equal basis with all the onscreen pixels; however, such a pixel simply does not get displayed. If I sprang for a monitor that was fifteen inches wide, the computer would display the pixel at the far right edge. As far as the computer is concerned, it's up to me, the user. The "hypothetical" pixel which would be displayed if I bought a bigger monitor remains part of the computer's memory in just the same way as the "real" pixel which can be and, therefore, is displayed.

     So we see that, in computer terms, a "property" may be thought of as the value of a variable needed to complete the description or definition of a unit of information such as a pixel. In other words, the number that the computer uses to fill in a required blank. And we see that this way of operating allows for a great deal of flexibility in the way that the computer can choose to handle any given property -- in particular, whether or not it is displayed -- without restricting the underlying programming. Finally, we see that this way of dealing with properties is an efficient way of handling huge amounts of information -- vast numbers of "particles" which are both identical in definition and individually unique in value -- using simple definitions and instructions.

Building a model of the universe. From the parts described in this chapter, we can begin to build a model of the universe as though it were run by a cosmic computer. Quantum waves behave much more like waves generated by a computer than like physical waves. Quantum properties are much more like variables in a computer's formulas than like physical properties. And quantum "particles" are very much like the evanescent dots on your computer screen which are here when you need them and tucked away in memory when you don't...