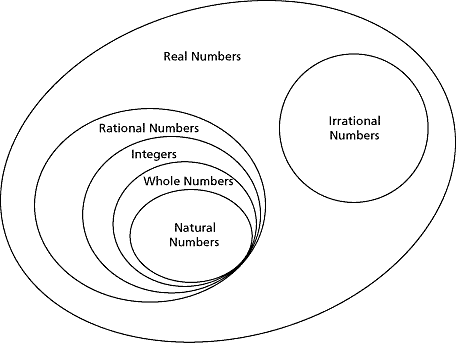
Word Gems: Mathematics: Notes: Whole Number

Have you ever wondered, "What are whole numbers in math?" If so, you're not alone. Whole numbers are an important concept in mathematics, and understanding them can help you solve various problems.

In this blog post, we'll take a closer look at whole numbers and how they can be used in mathematical equations. By the end, you should have a better understanding of this important topic. So let's get started!

What are whole numbers?

Whole numbers are a type of number used for counting, ordering, and measuring in mathematics. Most of the time, they don't have fractions or decimals and go from 0 to infinity.

Whole numbers are one of the most fundamental types of numbers, and basic arithmetic operations such as addition and multiplication can be applied to them; this makes them incredibly versatile.

Whole numbers also have certain properties that make them unique compared to other types of numbers, including commutativity, which means the order in which operations occur between two whole numbers doesn’t impact the final result.

What is the definition of a whole number?

Whole numbers are a basic type of math structure that is used to count and describe amounts. Examples of whole numbers include any positive integer, such as 1, 2, 3, 4, 10, 500, or 7 million.

Whole numbers can't be changed. They have a fixed value and don't have any fractional or decimal parts. This makes them ideal for representing discrete values, such as the number of people in a room or the number of apples in a basket.

Whole numbers are also known for the fact that they follow some basic math rules, like adding and multiplying. These operations adhere to commutative properties, meaning that the order in which they take place doesn’t affect the final result.

For example, if you add 3 and 5, it doesn’t matter if you start with 3 or 5; the result will always be 8.

Even in more complicated equations, whole numbers still follow the basic rules of math, which makes them useful for making calculations and formulas.

What are the properties of whole numbers?

Whole numbers, also known as natural numbers, are a subset of integers. When compared to other types of numbers, beginning with the number zero and including counting numbers such as one, two, three, and so on, they have few properties.

One of the most important properties of numbers is that whole numbers can always be divided by themselves (apart from zero) to give a result of one. As a consequence of this property, every whole number must be greater than 0 but not equal to it.

Mathematicians often compare whole numbers to fractions or decimals to learn more about how they work. In comparison with fractional numbers, whole numbers have no fractional parts and have an infinite number of decimal places up to any chosen digit.

Lastly, other math operations, like division, can produce results that are not whole. However, they are all linked by the basic idea that adding any two whole numbers together makes a new whole number.

What is the difference between whole numbers and natural numbers?

The difference between whole numbers and natural numbers is that whole numbers include 0, while natural numbers do not.

In other words, natural numbers are positive integers greater than zero (1, 2, 3, etc.), while whole numbers include all non-negative integers, including zero (0, 1, 2, 3, etc.).

Therefore, when talking about counting numbers, the term “natural number” is often used to refer to the set of positive integers. But the term "whole number" is usually used when talking about all non-negative integers, including 0.

Additionally, whole numbers are commonly used in mathematical operations like addition and subtraction due to their inherent property of "closure," which means that when two whole numbers are added or subtracted, the result is always a whole number. This makes it easy to calculate with them since you can be certain of the outcome.

In summary, natural numbers refer to positive integers greater than zero, while whole numbers include all non

The difference between whole numbers and natural numbers is that whole numbers include 0, while natural numbers do not.

In other words, natural numbers are positive integers greater than zero (1, 2, 3, etc.), while whole numbers include all non-negative integers, including zero (0, 1, 2, 3, etc.).

What is not a whole number?

Numbers that include incomplete parts, such as fractions and decimals, are not whole numbers. Some examples are 2.5, 4.7, 3/4, and 5/6.

What is a whole number in math?

In math, a whole number is a number from zero to infinity that does not include any decimals or fractions.

Is 0 A whole number?

Zero is both a whole number and an integer. It is not a natural, or counting, number, because it is not a number used to count physical objects.

What are the whole numbers from 1 to 10?

The whole numbers from 1 to 10 are as follows: 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.